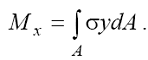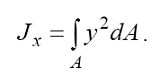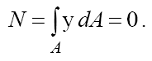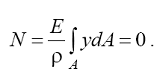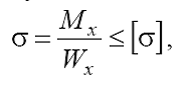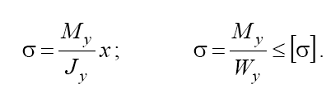Лаборатория Механических испытаний

Прочность—залог успеха

ЗГИН

1. Основні поняття

Під згином розуміється такий вид навантаження, при якому в поперечних перерізах стержня виникають згинаючі моменти. Поряд зі згинаючими моментами при згині в більшості випадків виникають і поперечні зусилля.

Чистий згин – деформація, при якій в поперечних перерізах стержня діє тільки згинаючий момент.

Поперечний згин – деформація, при якій в поперечних перерізах стержня діють одночасно згинаючі моменти і поперечні зусилля.

Якщо зовнішнє навантаження розташоване у площині, що проходить через одну з головних центральних осей інерції цього перерізу (зокрема – вісь симетрії), то балка деформується в цій же площині. Такий згин називають прямим або плоским.

На рисунку 1 зображений брус, підданий прямому згину. Згин викликається дією сил і моментів, які лежать у силовій площині П, що проходить через поздовжню вісь балки.

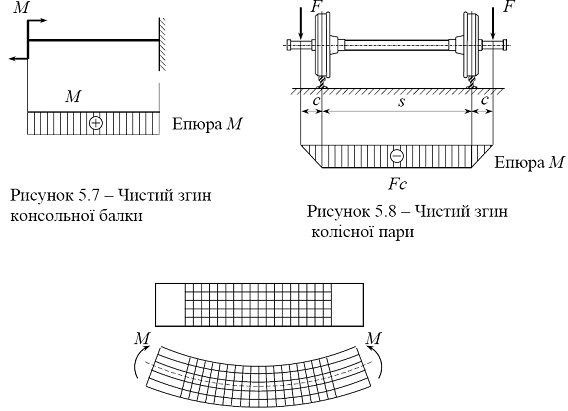
Рисунок 1 – Прямий згин бруса

В умовах згину працюють рейки залізничної колії, хребтові балки вагонів, оси колісних пар, вали зубчастих передач, елементи мостів і мостових перекриттів і т.п. Стержень, що працює на згин, називають балкою.

2. Нормальні напруження при прямому чистому згині

При чистому згині в поперечних перерізах балки діють тільки згинаючі моменти M_x , інші внутрішні силові фактори відсутні, в тому числі і поперечне зусилля Q_y = 0.

В цьому випадку, із залежності (5.6) витікає, що при чистому згині згинаючий момент на цій ділянці балки постійний : M_x = const.

Прикладом деформації чистого згину являється балка з защемленням під дією зосередженого моменту (рисунок 1), або вісь колісної пари вагону (рисунок 2). В обох випадках вага самих балок не враховується.

Розглянемо деформацію чистого згину гумової моделі балки прямокутного перерізу, на бічну поверхню якої нанесена прямокутна сітка (рисунок 5.9). По торцям балки прикладемо два моменти М . методом перерізів неважко встановити, що в усіх перерізах балки діє постійний згинаючий момент М_х = М, а поперечне зусилля Q_y = 0.

Рисунок 4 – Деформація чистого згину гумової моделі балки

Під навантаженням поздовжня вісь і поздовжні лінії сітки зігнуться по дугам окружностей (в усіх перерізах діє один і той же згинаючий момент, тобто, радіуси кривизни поздовжніх ліній в усіх перерізах повинні бути однакові), поперечні лінії не викривлюючись, повернуться на деякі кути, залишаючись перпендикулярними поздовжнім лініям. Довжина середньої поздовжньої лінії не зміниться, розташовані вище неї поздовжні лінії видовжаться, а розташовані нижче – скоротяться.

Якщо припустити, що внутрішні деформації балки мають той же характер, що і на поверхні, то при чистому згині :

• справедлива гіпотеза плоских перерізів (поперечні перерізи балки, плоскі і нормальні до поздовжньої осі до прикладення навантаження, залишаються такими ж і при його дії);

• відсутній тиск волокон одне на інше (оскільки відсутнє поперечне зусилля);

• в поперечних перерізах діють тільки нормальні напруження (оскільки змінюються довжини волокон).

Рисунок 4—Нормальні напруження при чистому згині

Залежність між згинаючими моментами і нормальними напруженнями в перерізі балки :

                                                                                                

Розподіл нормальних напружень визначимо по відносним деформаціям і закону Гука:

                                  

Інтеграл у цьому виразі називається осьовим моментом інерції перерізу. Він позначається :

      .

Звідси величина, обернена радіусу кривизни осі балки :        

Після підстановок отримаємо формулу для визначення нормальних напружень в перерізі балки в залежності від згинаючого моменту

.      

Із цієї формули витікає, що нормальні напруження в довільній точці поперечного перерізу прямо пропорційні її відстані у від нейтральної осі, тобто лінійно змінюються по висоті перерізу. Від координати х перерізу напруження не залежать, тобто по ширині перерізу нормальні напруження незмінні.

В перерізі балки є нейтральна вісь (або нульова лінія) в якій нормальні напруження рівні нулю. Відзначимо, що досі її положення було прийнято довільно: це координатна вісь О_x, що співпадає з віссю симетрії перерізу балки.

Положення нейтральної осі визначимо із умови, що поздовжня сила N в перерізі дорівнює нулю :

     

Підставивши в (5.16) значення нормального напруження із (5.15), отримаємо :

Відношення Е/ρ ≠ 0, так як радіус кривизни не дорівнює нескінченності : ρ ≠ ∞ (реальна балка деформована, її вісь зігнута).

Інтеграл в останній залежності називається статичним моментом площі перерізу відносно осі х, він позначається Sх .

Виконання цієї умови можливе, якщо статичний момент дорівнює нулю:

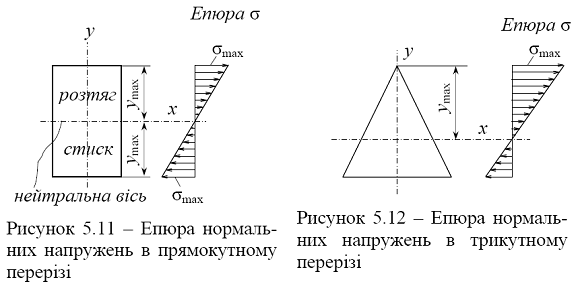
Це означає, що вісь Ох проходить через центр ваги поперечного перерізу і тому вісь х являється нейтральною.

Епюра розподілу нормальних напружень по перерізу балки прямокутного перерізу приведена на рисунку 5.11. Нейтральна вісь ділить переріз на дві зони : в одній виникають нормальні напруження, що розтягують , в другій – стискаючі. На нейтральній осі нормальні напруження рівні нулю.

В прикладі, що розглядається, верхні волокна балки розтягуються, нижні – стискаються).

При прямому згині балка з поперечним перерізом, що має одну вісь симетрії, положення нейтральної осі визначається із умови (5.17). На рисунку 5.12 приведена епюра напружень в балці трикутного поперечного перерізу.

В точках з координатою у = у_mах в перерізі діють максимальні напруження :

,

де позначимо :

Величина Wx називається осьовим моментом опору перерізу відносно осі х.

Умова міцності при чистому згині :

де [σ] – допустиме нормальне напруження при згині ; визначається по результатах дослідження матеріалів.

При згині балки відносно осі у розрахункові формули відрізняються індексами і координатою:

 

Смотри также